Basic Math Formulas: Practice Made Easy
To Memorize or Not to Memorize
Once you master basic math formulas you’ll find finishing homework and acing tests much easier. Memorization is not enough and may not even be necessary for mastery. Mastery involves knowing when and how to use a formula. For example, you might be asked to find the area of a triangle (yes, there are real world applications for this; trust me), and since you memorized the formula for the area of a rectangle and used it, your calculations are way, way off.
Although memorizing a formula can make your life easier, you don’t need to memorize them to master them. You will discover, however, that frequent use of a formula will lead to memorization.
By the way, if your math teacher requires you to memorize formulas–notwithstanding that people in the real world use charts and (gasp!) cheat sheets in case they forget–humor him or her and memorize the darn things, while keeping in mind what’s most important: mastery.
Geometric Shapes: Basic Formulas
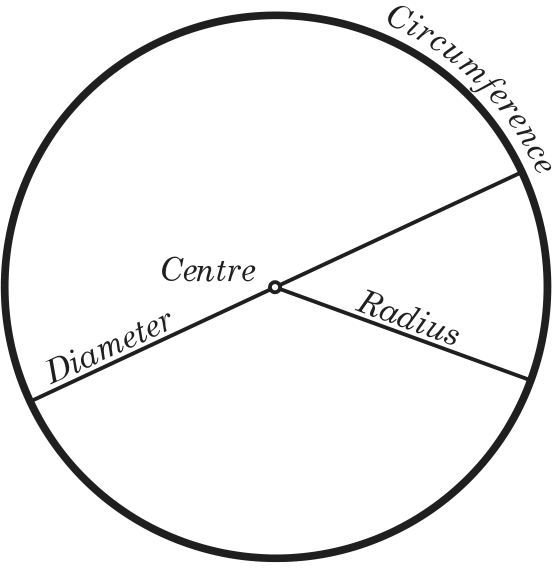
Circle
- Area = ∏r2
- Circumference = 2∏r
Square
- Area = length * width
- Perimeter = 4 * length
Rectangle
- Area = length * width
- Perimeter = 2*length + 2*width
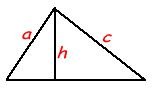
Triangle
- Area = 1/2 * base * height
- Perimeter = a + b + c
- Pythagorean Theorem (right triangles only) - a2 + b2 = c2
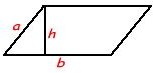
Parallelogram
- Area = base * height
- Perimeter = 2*a + 2*b
Trapezoid
- Perimeter = side a + side b1 + side b2 + side c
- Area = height * (side b1 + side b2) / 2
**
Three Dimensional Formulas
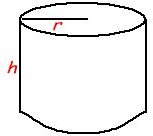
Cylinder
- Surface Area = (2 * ∏ * r2 ) + (2 * ∏ * r * height)
- Volume = ∏ * r2 * height
Cube
- Surface Area = 6 * length2
- Volume = length3
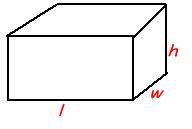
Three dimensional Rectangle
- Surface Area = 2 *length * width + 2 * length * height + 2 * width * height
- Volume = length * width * height
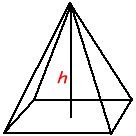
Pyramid
- Volume = 1/3 base * height
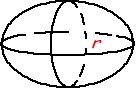
Sphere
- Volume = 4/3 * ∏ * r3
- Surface Area = 4 * ∏ * r2
Basic Algebra Formulas
- xa * xb = xa+b
- (xa)b = xab
- (xy)a = xaya
- (x+y)2 = x2 + 2xy + y2
- (x-y)2 = x2 - 2xy - y2
Other Math Formulas
Converting a Fraction to a Decimal - Numerator / Denominator- Slope of a Line - rise / run
- Slope Intercept Form - y = mx + b (if you don’t know what this means, go here for an explanation)
- Quadratic Formula - Given the formula ax2 + bx + c = 0, x can be solved with the following equation:
Solving Problems
Knowing and understanding the above formulas should be sufficient for passing any standardized math test, assuming you know when to use them. When determining which formula to use, make sure you read the question carefully and understand exactly what it is asking; otherwise, knowing the formula will do you no good. Once you understand what the question is asking and determining which formula to use, be sure to list all necessary information.
The next article in this series will give you a step-by-step explanation on how to solve math problems.
This post is part of the series: Solving Math Problems the Easy Way
Math isn’t as hard as you think it is.
