How to Find the Diameter of a Circle

Necessary Definitions

Before learning how to find the diameter of a circle, it's necessary to know the following definitions:

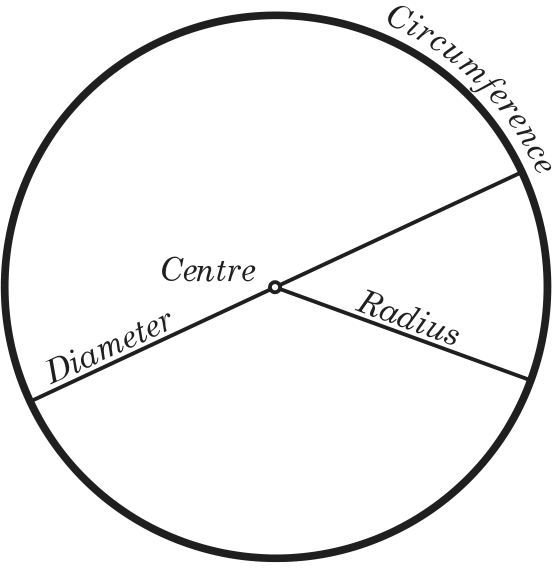
Diameter of a Circle – a straight line that passes through the center of the circle and touches two opposite sides.
Radius – a straight line from the center of a circle to any point on the circle's perimeter.
Circumference – a fancy word for the circle's perimeter or boundary.
Area of a Circle – the total surface of the circle. The area's measurement will always be squared–in², ft², m², for example.
Center of a Circle – the point inside the circle that is the same exact distance from every point on the circle's perimeter.
Pi/∏ – the number pi goes on indefinitely. For our purposes we'll stop at the 1/100 slot. For these calculations, pi will be 3.14.

Calculating a Circle’s Diameter

How to find the circle's diameter depends on the information available.

If the circle is drawn to scale or if it's an actual circle, you can calculate the diameter by measuring from one side of the circle to another, making sure the ruler passes through the circle's center. Because finding the exact center may prove difficult, it's best to take several measurements to ensure accuracy.
If you know the radius of the circle, multiply it by 2 to find the diameter.
- If the radius of a circle is 2.47 cm, the diameter is 2.47 cm * 2, which equals 4.94 cm.
If you know the circumference of a circle you can divide it by pi (3.14) to get the diameter (circumference = pi * diameter).
- If the circumference of a circle is 6.28 inches, the diameter is 6.28 inches / 3.14, which equals 2.
If you know the area of a circle, you must manipulate the formula of a circle's area by doing the following:
1. Know the formula for the area of a circle–Area = pi * radius²(A=∏r²).
2. Solve for the radius by dividing both sides by 3.14 (pi) and taking the square root. The resulting formula is radius = the square root of the area/pi
3. Once you know the area, multiply it by 2 to get the diameter.
Here's an example of how to find the diameter of a circle if the circle's area is given:
- If the area of a circle is 12.56 m², the radius = the square root of 12.56 meters²/3.14. 12.56 meters²/3.14=4 meters². The square root of 4 meters²equals 2 meters.
- If the radius of a circle equals 2 meters, multiply it by 2 to get the diameter. The diameter of a circle in this example is 4 meters.

Formula Recap

Diameter = 2 * radius
Diameter = circumference / pi
Diameter = 2(square root of the area/pi)

Now you can figure out the diameter of a circle as long as you know the radius or the circumference or the area.

Public domain images courtesy of wikimedia commons.

This post is part of the series: Solving Math Problems the Easy Way

Math isn’t as hard as you think it is.