Solve Area of A Triangle Problems With the Pythagorean Theorem
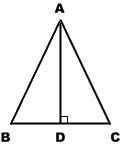
Area of an Isosceles Triangle
This article will cover a few area of a triangle problems to help you solve area of Isosceles and Scalene triangles.
[caption id="" align=“alignnone” width=“600”]
An isosceles triangle has two equal sides. If you know the length of all the sides, you can find the area of an isosceles triangle with the help of the Pythagorean theorem. The formula for area of a triangle with base b and height h is A = ½_bh_ To find the area of an isosceles triangle ABC, use the unequal side, BC, as the base. The height, AD, intersects the base at the midline and creates two congruent right triangles. The one on the left has hypotenuse AB and leg BD. BD is equal to ½_BC_. Since the hypotenuse and one leg are known, the Pythagorean theorem can be used to find the length of the third leg, AD, which is also the height of the isosceles triangle. Area of a Triangle Problems - Finding the area of an isosceles triangle An isosceles has two sides with length 25 cm and a third side with length 30 cm. What is its area? How to solve: Step 1. Draw a line segment from the unequal side to the opposite angle. This line is equal to the height and also creates two small right triangles. Step 2. Find the length of the new line segment using the Pythagorean theorem. _a_² + _b_² = _c_² _a_² + ((½)(30))² = 25² (Why ½ times 30? The short leg is one half of the base of the isosceles triangle.) _a_² + 15² = 25² (Remember order of operations. Find the value in parentheses before using exponents outside the parentheses.) _a_² + 225 = 625 _a_² = 400 (Subtract 225 from both sides.) a = 20 (Find the square root of both sides.) Step 3. Find the area of the isosceles triangle using the triangle area formula. Use the value of a from Step 2 as the height. A = ½(30)(20) A = 300 square inches
Area of Scalene Triangle
A scalene triangle has three unequal sides. To find its area without knowing its height, you need to know the length of two sides, plus one more value. The height—a perpendicular line segment from the base to the opposite angle—does not divide the base into two equal portions. To calculate the height, you also need the distance along the base from this line segment to one end of the base. Area of a Triangle Problems - Finding the area of a scalene triangle
[caption id="" align=“aligncenter” width=“600”]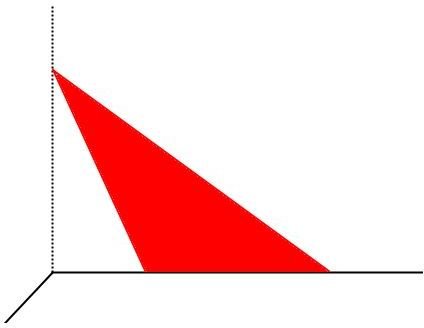
Scalene triangle[/caption]
Someone has painted a mural of a red scalene triangle on a wall (click on the diagram to enlarge it). One corner of the triangle touches the corner between two walls. You decide to paint over it, but you only have a enough white paint to cover 4000 square inches. You already know that the left side is 85 inches long, but you cannot reach high enough to measure the height. So instead, you measure the base (80 inches) and the distance from the base of the triangle to the wall (36 inches). Do you have enough paint? How to solve: To solve this problem, look for right triangles so you can use the Pythagorean theorem to find the area. Step 1. Notice that the red triangle forms a smaller white triangle with the side and bottom of the wall. You know the corner is a right angle, so this is a right triangle. Its base is 36 inches and its hypotenuse is 85 inches. Step 2. Find the height using the Pythagorean theorem. _a_² + _b_² = _c_² _a_² + 36² = 85² (Cool fact: to square these numbers without a calculator, you can use Vedic mathematics!) _a_² + 1296 = 7225 _a_² = 5929 (Subtract 1296 from both sides.) a = 77 (Find the square root of both sides—you will need a calculator.) Step 3. Calculate the area of the red triangle using the area formula for triangles. Use a from Step 2 as the height. A = ½(77)(80) A = 3080 square inches Your 4000 square inches’ worth of white paint will be enough to cover the 3080 square inch red triangle. References: You can also type “area of a triangle” into Google.com and Google will give you a little calculator to assist.
