Speed Multiplication Using Vedic Mathematics: Arithmetic Simplified
Vedic Mathematics is a system of mathematical working and reasoning based on the ancient Indian teachings called Veda. It is an ancient technique, which simplifies multiplication, divisibility, complex numbers, squaring, cubing, and square and cube roots. Even recurring decimals and auxiliary fractions can be handled by Vedic mathematics. It is different from conventional mathematical methods in terms of the time it takes. With the help of Vedic mathematics, problems can be solved in less steps, at a much faster rate and even mentally. The basis of Vedic Mathematics, are the 16 Sutras, which attribute a set of qualities to a number or a group of numbers.
Techniques to Try
There are several VM techniques which are easy to learn and will empower you to do some very particular mathematical problems at great speed.
For example, to find the square of a number ending in five:
Squaring 65:
Step 1: Determine the number on the left of 5 (in this case the number is 6).
Step 2: Multiply the number in step 1 with its successive natural number, i.e. 6*(6+1) = 6*7.
Step 3: Write (5*5 = 25) at the end of the number obtained in step 2.
So, the answer in this case is 4,225.
On a similar basis, try squaring other numbers like 25, 35, 75, 85, 105 (in the case of 105, the number at the left of 5 is 10. Now multiply 10 with (10+1) and the final result is 11,025).
The above method can be generalized for multiplication of any two digit numbers which satisfy these two conditions:
- the same digit at the tens place, and
- the digits at units place add to 10.
For example,
Multiply 43 and 47:
Step 1: Determine the number at the tens place and multiply it with the next consecutive natural number in the number series. In this case, 4*(4+1) = 4*5 = 20.
Step 2: Multiply the numbers at the units place (the numbers whose sum is 10), here 3 and 7.
Step 3: The numbers in step 1 and step 2 writing adjacently is your answer, 2,021.
Try multiplying 52 and 58, 91 and 99, 106 and 104 as an exercise.
The main advantage of these techniques is you don’t need to use pen and paper. After practicing for a while, you can do them mentally. To spice up things, challenge your friends to mentally multiply, say 103 and 107, or square 95, and see who does it in the least amount of time. We will learn more such methods which though being specific, allow you to solve a wide range of algebraic problems in a blink.
Now let us see a very general method to multiply any two whole numbers. The method might require you to use pen and paper, but the number of operations involved and time is hugely reduced and hence the chances of error are also diminished.
Method for Multiplying Two Whole Numbers
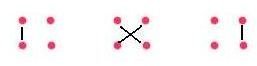
Let us study this method with an example: 63*48
We will be doing multiplication with the vertical and crosswise method.
The method is schematically represented above,
Step 1: Write the numbers one below another and multiply the digits at units place.
63
48
-————
Here, 3*8 = 24. So the units place of the answer has 4, and 2 is the carry forward.
Step 2: Now, cross-multiply the digits as shown in the diagram, and add the two numbers obtained after multiplication,
6*8 = 48 and 4*3 = 12
48 + 12 = 60
Step 3: The number obtained is 60. Adding the carry forward from step 1, we get, 60 + 2 = 62.
Hence, the number at tens place of the answer is 2, and 6 is the carry forward for the next step.
Step 4: Now multiply the digits at the tens place and add the carry forward from step 3 to it.
6*4 = 24
24+6 = 30
So, our final answer is 3,024.
The method might seem tedious, but in reality all you had to write down were the two numbers one below the other, and your final answer. In the first step, the multiplication of two single digits can be done mentally, and 4 can be directly written in the unit’s place of the answer. The carry forward might be written as a subscript, so that it is not forgotten. Even in the second step multiplication and addition should come in your mental work and only the final tens place digit, 6, needs to be written down. The last step is similar to the first one, except for the addition of carry.
Do not be disheartened with the length of this method. It is only a matter of time before you get acquainted with it. Practice the method on more than two or less than two digit numbers, like 13*47, 76*8 (in this case, write the two numbers as 76 and 08, one below the other). Once you have mastered the method, you will find how fast and easily you can now do the multiplication, and then you won’t even need to write down anything on the paper. Try it!
This method can be generalized for multiplication of any two numbers. At the end of this page is the schematic diagram for up to 4x4 Vedic multiplications.
Do not forget to practice the above methods or else they won’t be of any use. You need to incorporate these methods in your daily calculations, so that you can master them and make yourself faster and more efficient at math.
Verifying Your Answer
No one is immune from errors, and quick ways of checking long computations are always useful. Below, I’m mentioning a method to verify your answer, so that the chance of error is minimized.
Suppose you have to verify that 8,216*4,215 = 34,630,440.
Step 1: Add up the digits of each factor (the numbers you want to multiply) and of the product.
Step 2: Divide each of the sum of digits by 9, and write down the remainder in each case – the remainder is called the check number.
Step 3: Now multiply the check numbers of multiplicand and multiplier. Add the digits of this product. The sum should be same as the check number of the product of your original multiplication, i.e. of 34,630,440.
8 + 2 + 1+ 6 = 17, check number is 8 (17/9 gives remainder to be 8).
4 + 2 + 1 + 5 = 12, check number is 3.
Now, 8*3 = 24. The sum of digits of this product is 2 + 4 = 6.
Now, verifying whether this is equal to the check number of the product.
Check number of the product is,
3 + 4 + 6 + 3 + 0 +4 + 4 + 0 =24, check number is 6.
Thus, the answer 34,630,440 is correct.
Images