Learn About the Intercept Theorem & Geometry Theorem Proofs of the Intercept Concept

The intercept theorem is an important elementary geometry theorem. It is very useful for solving the geometric problems related to the ratios of various line segments.

What is the Intercept Theorem?

The theorem states that if two or more parallel lines are intersected by two self intersecting lines, then the ratios of the line segments of the first intersecting line is equal to the ratio of the similar line segments of the second intersecting line. Bit confused? Ok, let’s explain it using the following example:

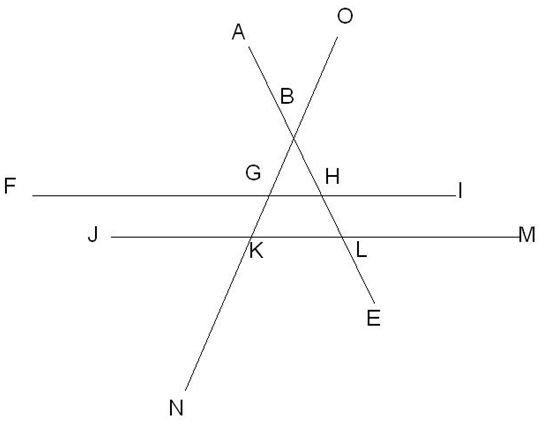
In the figure above, two parallel lines FI and JM are cut by two self intersecting lines AE and ON. Two triangles are formed as a result of the intersections of the lines. According to the intercept theorem, the ratio of the line segments created from ON should be equal to the ratio of the lengths of the line segments created from AE. Therefore,

|BG|: |GK| = |BH|:|HL|

The Geometry Theorem Proof

• From the above figure, it is clear that the ΔBGH and ΔBKL are similar.
• From the rules of similar triangle, we can write:

BK/BG = BL/BH………….eqn.1

• Now, we can write, BK=BG+GK and BL=BH+HL
• So, from the eqn.1 we can get:

(BG+GK)/BG = (BH+HL)/BH

Or, 1+ (GK/BG) = 1+ (HL/BH)

Or, GK/BG = HL/BH

Or, |BG|: |GK| = |BH|:|HL|

Practice Problem

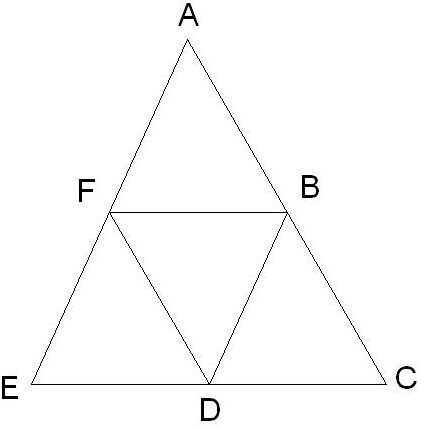
Problem: If the points B, D and F are the mid-points of the lines AC, CE and AE respectively, then prove that:

Area of ΔAFB = Area of ΔFED

Solution:

• Since the points F and B are the mid-points of the lines AE and AC respectively, so:

AF/FE = AB/BC

• Hence, the lines BF and EC must be parallel (according to the intercept theorem).

• Similarly, the lines BD and AE are parallel.

  Advertisement

• So, for the quadrilateral BDEF all the opposite sides are parallel to each other. Hence, the quadrilateral BDEF is a parallelogram with ED as one of the diagonal.

Hence, Area of ΔEFD = Area of ΔBDF……….eqn2

• Similarly, the quadrilateral ABDF is also a parallelogram with BF as one of the diagonal.

Hence, Area of ΔABF = Area of ΔBDF………eqn3

• From the Eqn.2 &3, it can be prove that:

Area of ΔAFB = Area of ΔFED

I hope this has helped you better understand the important concept of the theorem. Knowing this will help when implementing the theorem for different geometric problems.