Math Help: Pythagoras Theorem and Theorem Proofs

Around 2530 years ago, Pythagoras first created the Pythagorean Theorem. A simple Pythagorean Theorem proof is making a pyramid with a perfect square or rectangular base.

The Theorem

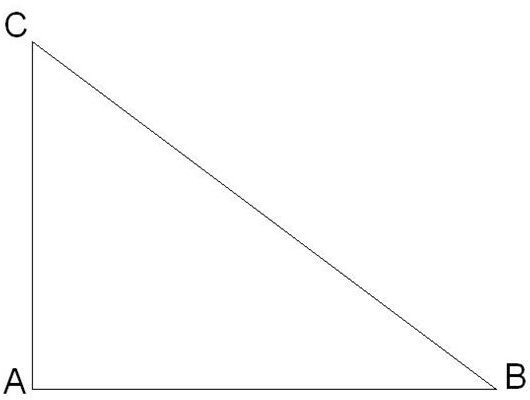
The square of the hypotenuse of a right angled triangle is equal to the sum of squares of other two sides.

See the attached snap of the triangle below (Click on it to enlarge):

So, as per Pythagoras theorem we can write that:

(BC)2 = (AB)2 + (AC)2

If we consider the side AB as a, AC as c and BC as b then we can write the Pythagorean Theorem as

b2=a2+ c2

Now you are in a position to calculate the length of any one side of a right angled triangle, if the lengths of the other two sides are given.

Practice Problems

Solve the following examples. Assume c is the hypotenuse of a right angled triangle and a, b are the other two sides of the same triangle:

a = 3; b = 4; c=?

a=5; c= 13; b=?

a=8; b=15; c=?

a= 9; c=41; b=?

Pythagorean Theorem Proof

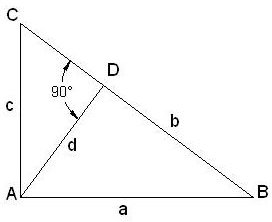
Pythagoras’ Theorem has more than 300 proofs. The simplest proof of the theorem is based on the similar triangles concept:

• Take the triangle ABC with AB=a, AC=c and BC=b.
• Drop a line from A to D which is perpendicular to BC.
• Consider AD=d.
• Triangle ACD is similar to the triangle ABC as:

Angle ADC = Angle CAB = 90 degree

Angle ACD = Angle ACB

Side AC is common for both the triangle

So, we can write from similar triangle principle:

c / b = DC / c

c2 = b X DC …………….eqn.1

• Again, triangle ABD and triangle ABC are similar because:

Angle ADB = Angle CAB = 90 degree

Angle ABD = Angle ABC

Side AB is common for both triangles.

So, we can write:

a / b = BD / a

a2 = b X BD …………….eqn.2

• From eqn.1 and eqn.2 we can write:

c2 +a2 = (b X DC) + (b X BD)

= b X (DC + BD)

= b X BC(as, BC consists of DC and BD)

= b X b(as, we already assume BC=b)

= b2

Real Life Examples

• Making a perfect rectangular basketball and volleyball court.
• Measuring the height of ramp.
• Calculating distance between two points if co-ordinates of the points are given.

Pythagoras Triples

Pythagoras triples are sets of three integer numbers which follows Pythagoras’ Theorem. For example, take 3, 4, 5.

Remember the Pythagoras theorem (b2=a2+ c2).

Now, if you take a=3, c=4 then from the theorem b will be equal to 5. There are many such sets of integers like this: 5, 12,13; 17, 24, 25; 9, 40, 41 etc.

People have been using these triples even before human beings learned to write.