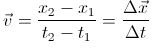How to Calculate Velocity: Average and Instantaneous
Speed vs. Velocity
Before beginning a discussion on how to calculate velocity, it is first necessary to clear the common confusion that young physics students typically have about speed and velocity. Speed is a scalar quantity, which means it only has a magnitude and no direction. On the other hand, velocity is a vector quantify, which means it has both a magnitude and a direction.
For the purpose of introducing the concepts of average and instantaneous velocity in an easy-to-understand way, I will be focusing on a one-dimensional analysis of velocity.
Average Velocity
When defining the motion of an object, a useful description is the change of the object’s position over a specified time period. Taking an example of a moving particle, suppose that 2.0 s after it starts moving it is at point _P_1, 15 m from the origin, and 5.0 s after it starts moving it is at point _P_2, 75 m from the origin. The displacement of the particle would be a vector from _P_1 to _P_2, and would measure (75 m – 15 m) = 60 m. The time period would measure (5.0 s – 2.0 s) = 3.0 s. Therefore, the particle’s average velocity during this time period is equal to the particle’s displacement divided by the time period: (60 m)/(3.0 s) = 20 m/s.
As you may have noticed, the average velocity of the particle depends on the time interval in which we consider its displacement. For instance, if we considered a 2.0 s time interval before the particle started to move, the particle’s average velocity would be zero since it would have no displacement. Therefore, it is necessary to generalize the definition of average velocity. At time _t_1, the particle is at _P_1 with distance _x_1. At time _t_2, the particle is at _P_2 with distance x_2. The displacement of the particle, denoted Δ_x, is the change in the distances of the two positions and is calculated as follows: Δ_x = x_2 - _x_1
The average velocity is equal to the displacement divided by the time interval:
For more examples on how to calculate average velocity, check out the velocity formula study guide.
Instantaneous Velocity
Although average velocity is useful in describing the motion of an object over a certain time interval, it can’t describe the motion of an object at an instant in time during the interval. For this, a new description on how to calculate velocity needs to be defined, called instantaneous velocity. In order to find the instantaneous velocity of the particle previously discussed at point P_1, we must move point P_2 closer to point P_1 and calculate the average velocities between the two points as they become exceedingly closer. As Δ_x and Δ_t become smaller, the ratio Δ_x/Δ_t_ will reach a “limit.” Therefore, the instantaneous velocity is the limit of the average velocity as the time interval approaches zero:
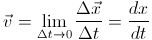
References
- University Physics with Modern Physics, 12th ed. / Hugh D. Young…[et al.].