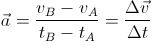A Guide on How to Calculate Acceleration: Average and Instantaneous
What is Acceleration?
You most likely have heard of the term “acceleration” being used whenever listening to a sports commentary, such as auto racing, or whenever seeing the news about a spacecraft being launched into space. These would give you a vague idea of acceleration as a form of motion. However, there is an exact definition of acceleration in its physical sense and this can also be represented by mathematical equations.
In order to understand acceleration, you must first know about velocity. Just as velocity describes the rate of change of position with respect to time, acceleration describes the rate of change of velocity with respect to time. It is important not to confuse these two concepts. If you have trouble differentiating the two, it may be helpful to memorize the phrase “acceleration is to velocity as velocity is to position.” Also like velocity, acceleration is a vector quantity. This means that direction is considered with the magnitude.
Below, I will discuss how to calculate acceleration for two cases: average and instantaneous accelerations.
Average Acceleration
The simplest and most common type of acceleration you will encounter is average acceleration. This describes the acceleration of an object over the length of the path being considered. For instance, let’s consider a car traveling on a straight path and that the driver is pressing down on the gas pedal. When looking at average acceleration, we will always consider two points in time. So we will take arbitrary points A and B along the path, in which the car travels through A to B. We will assume that at point A 10 seconds have passed and the car is traveling 20 m/s, and at B 30 seconds have passed and the car is traveling 50 m/s. To calculate its average velocity we will use the following standard equation:
If we substitute our assumed values into the variables, we will have:
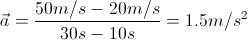
Therefore, the average acceleration of the car is 1.5 m/s2. Note that to get the units for acceleration, we take (m/s)/s, which gives us m/s2.
Instantaneous Acceleration
Depending on which level you are studying acceleration, you may or may not be expected to calculate instantaneous acceleration, as it requires basic knowledge of calculus. Nonetheless, I will briefly define instantaneous acceleration.
The term “instantaneous” is defined as occurring in an instant. Therefore, instantaneous acceleration is simply the acceleration of an object at an instant. Although this may seem to be contradicting the concept of average acceleration, which always considers two points in time, it actually isn’t. And this is where the calculus comes in.
One of the first concepts you learn in calculus is limits. In relation to acceleration, if we were to consider point A as introduced earlier, and then take point B to be closer and closer to A so that the average acceleration is calculated over shorter and shorter time intervals, we will get the limit of the average acceleration as the time interval approaches zero. And this is precisely instantaneous acceleration.
However, a more practical approach to calculating instantaneous acceleration is using derivatives. This also requires some basic knowledge of calculus. With this it is obvious that instantaneous acceleration is equal to the rate of change of instantaneous velocity with respect to time.
These results are shown as follows:
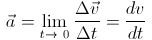
So far I have explained two specific types of acceleration, average and instantaneous, and went over how to calculate acceleration in these two cases. The best way to understand these concepts is to do practice questions. If you have a physics textbook, you can flip to the relevant chapter and do some of the questions they have at the end.
If you would like to see another example in which the acceleration formulas are used, you can take a look at the Acceleration Formula Study Guide.
References
- University Physics with Modern Physics, 12th ed. / Hugh D. Young…[et al.].