Protect Your Castle Using the Pythagorean Theorem: Eighth Grade Math Lesson
Long ago, people lived in castles. For protection from their enemies, they built moats around their castle. A moat made it very difficult for the enemies to reach the castle. The wider the moat, the more easily a castle could be defended. From narrow openings in the walls of the castle, archers shot their arrows to the enemies on the other side of the moat. What is the minimum distance the archer should be able to shoot his arrow to reach the enemies outside the castle?
Lesson Objective: The lesson is aligned to the Common Core State Standards for Mathematics - 8.G.7 Geometry - Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions.
Materials Required: graph paper, calculator
Lesson Procedure:
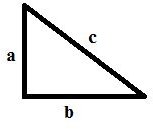
1. The narrow opening in the wall of the castle is 10 feet high. Draw a line segment to represent the height of the narrow opening in the castle wall. Label the line segment “a”.
2. The moat is 12 feet wide. Draw a line segment to represent the width of the moat. Label the line segment “b”.
3. Draw a right triangle. Use line segment “a” as side “a” and line segment “b” as side “b”. The third side of the triangle represents the minimum distance the archer needs to shoot his arrow. Label the third side “c”.
4. Your drawing should look like the right triangle below.
5. Use the Pythagorean Theorem a2 + b2 = c2, to find the length of side “c” of the right triangle. The length of side “c” is the minimum distance the archer needs to shoot his arrow. Calculate the length to the nearest tenth.
Answer: 15.6 feet
Individual or Group Work
Students should be able to apply the Pythagorean Theorem, a2 + b2 = c2, to determine unknown side lengths in right triangles in real-world problems with two-dimensional drawings. The following worksheet includes information about three different castles that shows the height of the narrow opening in the wall of the castle and the width of the moat. Students will need to find the minimum distance the archer needs to shoot his arrow to reach the enemies outside the castle and complete the table. Answers are also included.
<strong>Worksheet: Pythagorean Theorem Castle</strong>
This post is part of the series: Teaching the Pythagorean Theorem.
This series of lesson plans is intended for an eighth grade math class. Find a series of lessons that will teach your students about the Pythagorean theorem.
- Lesson 1: Explaining the Proof of the Pythagorean Theorem
- Lesson 2: Finding the Missing Lengths using the Pythagorean Theorem
- Lesson 3: Protecting the Castle using the Pythagorean Theorem
- Lesson 4: Hunting for Treasure using the Pythagorean Theorem
- Lesson 5: Playing a Video Game using the Pythagorean Theorem