Finding the Derivative of a Function in Calculus
What are Calculus Derivative Problems?
What is the derivative of a function?
The derivative measures the steepness of the graph of a function at some particular point on a graph. The derivative is a slope of a function. The general case for finding the slope of a tangent line or curve at any point can be found using the slope concept.
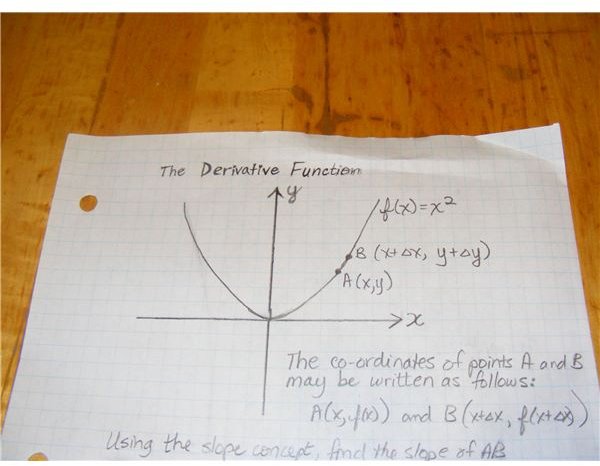
If you consider the function f(x) = x^2 and let A(x,y) be any point on the curve, you can then take a point B (x + D x, y + D y) where D x and D y are extremely small in value. ( D means delta. ) Examine the curve and the slope concept to find the slope of AB.
Below you will see that the slope of the curve, m, is represented by the expression 2x. By substitution for x, we can find the slope at any specific point.
Finding the Slope of a Curve

Finding the Derivative Using the Limit of the Change in Slope
The derivative of a function y= f(x) is the limit of the function as D x -> 0 and is written as:
Lim Dy/ Dx = lim [ f(x + Dx) – f(x) ]/( x + Dx – x )
D x->0 Dx ->0
To understand the concept of a limit, and solving a limit as x approaches 0, you can practice examples in the article How to Solve Calculus Limit Problems.
The above method of finding the derivative from the definition is called the Delta Process.
This method can be used to find the derivative of the following:
1. f(x) = 3x + 2
m = 3
2. f(x) = 3x2 – 2x + 1
m = 6x – 2
3. f(x) = -x2 – 5x + 1
m = -2x - 5
Examples of Finding the Derivative Using the Delta Process



Examples of Finding the Derivative Using the Power Rule
How to Find the Derivative Using The Power Rule
The delta process may be summarized into a short technique called the power rule:
If y = xn , then y’ = nxn-1
Note: There is different notation for the derivative of a function with respect to x:
y’
f’(x)
DxY
Dy/dx
D f(x)/dx
Examples for finding the derivative using the power rule:
1. y = 7x4
y’ = 28 x3
2. f(x) = 8/x5
f(x) = 8 x -5
f’(x) = -40 x -6
3. y = 3x2 -6x + px
y’ = 6x -6 + p
4. y = √x + 1/√x
y = x1/2 + x-1/2
y’ = ½ x-1/2 – ½ x-3/2
Examples of Finding the Derivative Using the Product Rule
How to Find the Derivative Using the Product Rule
Let f(x) and g(x) represent 2 functions:
D[ f(x) g(x) ] /dx= f(x) d[g(x)]/dx + g(x) d[f(x)]/dx
Or expressed another way: (f * g )’ = f * g’ + g * f’
Examples of finding the derivative using the product rule:
1. f (x) = 3x2 (√x – x )
f’(x) = (3x2)(1/2 x-1/2- 1) + (√x – x )( 6x)
2. f (x) = (4 – x2) ( 1/x + x )
f’(x) = (4 – x2) (-x-2 + 1 ) + ( 1/x + x ) ( -2x )
3. y = ( 3x2 ) (1 – x ) ( 7x3 – x )
y’ = (3x2 ) (1 – x ) ( 21x2 – 1 ) + (7x3 – x ) [( 3x2 )( -1) + ( 1 – x )(6x) ]
Finding the Derivative Using the Rules for Derivatives
There are several rules that are used in Calculus to find the derivative. This article provides examples using the power rule and the product rule. The constant rule, the quotient rule and the chain rule would be used to solve derivative problems also.
Most problems in Calculus use the basic rules for derivatives rather than the entire delta process to solve derivatives. Applying the proper rule to the Calculus problem is a skill students develop by practicing examples using all of the derivative rules. Review the basic Calculus Rules for Derivatives here.
Practice in Finding Derivatives
To practice several examples of finding the derivative using the power, product, quotient and chain rules, download the sample problems and solutions in Examples of How to Find the Derivative Using the Calculus Rules. These practice examples will help students to competently use and apply each rule to find the derivative.
Once these 4 rules are understood, the Calculus student can then go on to increasing their knowledge by learning the concept of integration. For more practice in both differentiation and integration, students may want to download a Calculus app for their iphone to help with more examples and practice tests. The article on The Best Iphone Math Apps describes this Calculus AB Review app.
Understanding and applying the concept of derivatives involves solving many examples. When these examples are then applied to problems such as acceleration problems, students can then put their basic problem solving skills to use in practical applications. This practice on how to find a derivative will help the students in Calculus to be confident problem solvers.
All content, including images, are from the author.
This post is part of the series: Solving Calculus Limit and Derivative Problems
This series shows how to solve several types of Calculus limit problems. Special cases of limits are solved and the related graphs are described. Solving Calculus limit and derivative problems are made understandable in this guide. See examples of how to find the derivative using derivative rules.